Bab 4 Matriks - Matematika Kelas 10 SMA/MA/SMK

Ringkasan Buku Sekolah
Kelas 10 (SMA / MA / SMK)
MATEMATIKA
Bab 4 Matriks

Latihan Soal dan Jawaban

Gambar .Ruang koleksi barang-barang pada suatu supermarket

Menemukan Konsep Matriks

Contoh

Pak Margono yang tinggal di kota P memiliki usaha jasa pengiriman barang.

Suatu ketika, perusahaan pak Margono menerima order mengirim barang ke kota V. Jika setiap dua kota yang terhubungkan diberi bobot 1, sedangkan dua kota yang tidak terhubungkan diberi bobot 0. Nyatakanlah persoalan pengiriman barang tersebut dalam bentuk matriks.

Gambar . Diagram rute pengiriman barang

Alternatif Penyelesaian

Kata kunci pada persoalan ini adalah keterhubungan antar dua kota, secara matematis, fungsi keterhubungan antar dua kota tersebut, dinyatakan sebagai berikut:

Dari gambar di atas, kota P terhubungan dengan semua kota, kecuali ke kota V.

Keterhubungan antar dua kota ini, dapat kita nyatakan dalam bentuk matriks seperti berikut.

Matriks representasi keterhubungan antar dua kota, disebut matriks X yang anggota-anggotanya terdiri dari angka 1 dan 0.

Jenis-Jenis Matriks

Matriks Baris

Matriks baris adalah matriks yang terdiri dari satu baris saja. Biasanya, ordo matriks seperti ini, 1 × n, dengan n banyak kolom pada matriks tersebut.

Matriks Kolom

Matriks kolom adalah matriks yang terdiri dari satu kolom saja. Matriks kolom berordo m × 1, dengan m banyak baris pada kolom matriks tersebut. Perhatikan matriks kolom berikut ini!

Matriks Persegipanjang

Matriks persegipanjang adalah matriks yang banyak barisnya tidak sama dengan banyak kolomnya. Matriks seperti ini memiliki ordo m × n.

Matriks Persegi

Matriks persegi adalah matriks yang mempunyai banyak baris dan kolom sama.

Matriks ini memiliki ordo n × n.

Matriks Segitiga

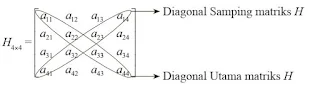
Mari kita perhatikan matriks F dan G berordo 4 × 4. Jika terdapat pola susunan pada suatu matriks persegi, misalnya:

maka matriks persegi yang berpola seperti matriks F dan G disebut matriks segitiga.

Jadi, matriks segitiga merupakan suatu matriks persegi berordo n × n dengan elemen-elemen matriks di bawah atau di atas diagonal utama semuanya nol.

Matriks Diagonal

Dengan memperhatikan konsep matriks segitiga di atas, jika kita cermati kombinasi pola tersebut pada suatu matriks persegi, seperti matriks berikut ini.

maka matriks persegi dengan pola “semua elemennya bernilai nol, kecuali elemen diagonal utama tidak semuanya bernilai nol”, disebut matriks diagonal.

Matriks Identitas

Matriks Nol

Jika elemen suatu matriks semuanya bernilai nol, seperti berikut:

Transpos Matriks

Kemandirian Dua Matriks

Definisi

Matriks A dan matriks B dikatakan sama (A = B), jika dan hanya jika:

i. Ordo matriks A sama dengan ordo matriks B.

ii. Setiap elemen yang seletak pada matriks A dan matriks B mempunyai nilai yang sama, a_ij = b_ij (untuk semua nilai i dan j).

Memahami Operasi Sederhana Matriks serta Menerapkannya dalam Pemecahan Masalah

Operasi Hitung pada Matriks

Penjumlahan Dua Matriks

Definisi

Misalkan A dan B adalah matriks berordo m × n dengan elemen-elemen a_ij dan b _ij. Jika matriks C adalah jumlah matriks A dengan matriks B, ditulis C = A + B, matriks C juga berordo m × n dengan elemen-elemen ditentukan oleh: c_ij = a_ij + b_ij (untuk semua i dan j).

Catatan:

Dua matriks dapat dijumlahkan hanya jika memiliki ordo yang sama. Ordo matriks hasil penjumlahan dua matriks adalah sama dengan memiliki ordo yang sama dengan matriks yang dijumlahkan.

Pengurangan Dua Matriks

Rumusan penjumlahan dua matriks di atas dapat kita terapkan untuk memahami konsep pengurangan matriks A dengan matriks B

Misalkan A dan B adalah matriks-matriks berordo m × n. Pengurangan matriks A dengan matriks B didefinisikan sebagai jumlah antara matriks A dengan lawan dari matriks –B, ditulis:

A – B = A + (–B).

Matriks –B dalam merupakan matriks yang elemennya berlawanan dengan setiap elemen yang bersesuaian matriks B.

Perkalian Suatu Bilangan Real dengan Matriks

Definisi

Misalkan A adalah suatu matriks berordo m × n dengan elemen-elemen a_ij dan k adalah suatu bilangan real. Matriks C adalah hasil perkalian bilangan real k terhadap matriks A, dinotasikan: C = k.A, bila matriks C berordo m × n dengan elemen-elemennya ditentukan oleh:

c _ij = k.a_ij (untuk semua i dan j).

Perkalian Dua Matriks

Jika C adalah matriks hasil perkalian matriks A_m×n terhadap matriks B_n×p, dinotasikan C = A × B, maka

• Matriks C berordo m × p.

• Elemen-elemen matriks C pada baris ke-i dan kolom ke-j, dinotasikan c_ij, diperoleh dengan cara mengalikan elemen baris ke-i dari matriks A terhadap elemen kolom ke-j dari matriks B, kemudian dijumlahkan. Dinotasikan c _ij = a _i1.b_1j + a_i2.b_2j + a_i3.b_3j + … + a _in.b _nj

Determinan dan Invers Matriks

Definisi

Misalkan A matriks berordo n × n. Matriks A^–1 adalah invers matriks A jika dan hanya jika A × A^–1 = A^–1 × A = I.

Ada beberapa cara untuk menentukan det.A, antara lain Metode Sarrus. Yaitu sebagai berikut:

MATERI-MATERI LAINNYA : 

Bab 1 Eksponen dan Logaritma 

Bab 2 Persamaan dan Pertidaksamaan Linier

Bab 3 Sistem Persamaan dan Pertidaksamaan Linier

Bab 4 Matriks

Bab 5 Relasi dan Fungsi 

Bab 6 Barisan dan Deret 

Bab 7 Persamaan dan Fungsi Kuadrat 

Bab 8 Trigonometri

Bab 9 Geometri

Bab 10 Limit Fungsi

Bab 11 Statistika

Bab 12 Peluang

Untuk melihat barang-barang bagus dan murah silahkan cek:

Promo Produk