Ringkasan Buku Sekolah
Kelas 10 (SMA / MA / SMK)
MATEMATIKA
Bab 3 Sistem Persamaan dan Pertidaksamaan Linier
Latihan Soal dan Jawaban
Menemukan Konsep Sistem Persamaan linear Dua Variabel
Anto bermain kartu bergambar bersama temannya. Ketika mereka selesai bermain, Budi, adiknya Anto mengumpulkan kartu-kartu tersebut. Kemudian Ia asyik membangun rumah bertingkat yang diberi nama Rumah Kartu. Susunan kartu untuk setiap tingkatnya dapat dicermati pada gambar berikut.
Gambar .Rumah Kartu Bertingkat
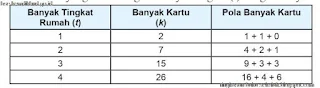
Rumah kartu bertingkat 1 mengunakan kartu sebanyak 2 buah.
Rumah kartu bertingkat 2 mengunakan kartu sebanyak 7 buah.
Rumah kartu bertingkat 3 mengunakan kartu sebanyak 15 buah.
Rumah kartu bertingkat 4 mengunakan kartu sebanyak 26 buah.
Temukan aturan yang memasangkan banyak tingkat (t) dengan banyak kartu (k).
Cermati pola, bahwa bilangan 1, 4, 9, 16 adalah kuadrat dari bilangan 1, 2, 3, 4 dan bilangan 1, 2, 3, 4 adalah banyaknya tingkat rumah. Apakah bilangan 0, 1, 3, dan 6 dapat dinyatakan dalam t2 dan t? Misal x dan y adalah bilangan yang akan ditentukan sekaitkan dengan banyak kartu dan banyak tingkat rumah yang dinyatakan dalam persamaan berikut.
k = x t2 + y t …………………………………………. (Persamaan-a)
Untuk t = 1 dan k = 2 diperoleh persamaan x + y = 2
Untuk t = 2 dan k = 7 diperoleh persamaan 4x + 2y = 7
Nilai x dan y dapat ditentukan sebagai berikut:
Evaluasi hasil yang diperoleh, apakah hasil yang diperoleh adalah solusi terbaik.
Dapat disimpulkan, aturan pengaitan banyak tingkat dengan banyak kartu yang digunakan untuk membangun rumah kartu adalah k = xt2 + yt dengan nilai konstanta 1 x dan y adalah 3/2 dan 1/2.
Tentukan banyak kartu yang digunakan membuat rumah kartu dengan 30 tingkat.
Jadi, banyak kartu yang dibutuhkan membangun rumah kartu bertingkat 30 adalah 1365 buah kartu.
Definisi
Sistem persamaan linear adalah himpunan beberapa persamaan linear yang saling terkait, dengan koefisien-koefisien persamaan adalah bilangan real.
Definisi
Sistem persamaan linear dua variabel (SPLDV) adalah suatu sistem persamaan linear dengan dua variabel.
Bentuk umum sistem persamaan linear dengan dua variabel x dan y adalah
dengan a1, a2, b1, b2, c1, dan c2 bilangan real; a1 dan b1 tidak keduanya 0; a2 dan b2 tidak keduanya 0.
x, y : variabel
a1, a2 : koefisien variabel x
b1, b2 : koefisien variabel y
c1, c2 : konstanta persamaan
Definisi
Sistem persamaan linear tiga variabel adalah suatu sistem persamaan linear dengan tiga variabel.
Notasi: Bentuk umum sistem persamaan linear dengan tiga variabel x, y, dan z adalah
Penyelesaian Sistem Persamaan Linier
Menentukan Himpunan Penyelesaian Sistem Persamaan linear Dua Variabel
Metode Grafik
Menarik garis lurus dari titik (0, 2) ke titik (2, 0) dan dari titik (0, 7/4) ke titik ( 7/4, 0).
Gambar .Grafik persamaan linear
Berdasarkan gambar grafik x + y = 2 dan 4x + 2y = 7, kedua garis lurus tersebut berpotongan pada sebuah titik, yaitu titik (3/2,1/2).
Sehingga himpunan penyelesaian sistem persamaan linear x + y = 2 dan 4x + 2y = 7 adalah{(3/2,1/2)}.
Metode Eliminasi
Metode eliminasi yang kamu kenal di SMP sudah kita terapkan terhadap SPLDV x + y = 2 dan 4x + 2y = 7 pada langkah penyelesaian Masalah-3.1.
Nilai x dan y dapat ditentukan sebagai berikut.
Metode Substitusi
Metode Eliminasi dan Substitusi
Menentukan Himpunan Penyelesaian Sistem Persamaan Linear Tiga Variabe
bentuk umum sistem persamaan linear dengan tiga variabel x, y, dan z adalah
Langkah-1: Eliminasi variabel x dari Persamaan-1 dan Persamaan-2
Langkah-2: Eliminasi variabel x dari Persamaan-1 dan Persamaan-3
Langkah-3: Eliminasi variabel y dari Persamaan-4 dan Persamaan-5
Dari hasil perkalian koefisien variabel y pada Persamaan-4 terhadap Persamaan-5 dan hasil perkalian koefisien variabel y pada Persamaan-5 terhadap Persamaan-4 maka diperoleh
Nilai variabel z di atas dapat dinyatakan sebagai hasil perkalian koefisien-koefisien variabel x, y dan konstanta pada sistem persamaan linear yang diketahui.
Dengan menggunakan cara menentukan nilai z, ditentukan nilai x dan y dengan cara berikut.
Sistem Pertidaksamaan Linear Dua Variabel
Contoh
Jika nilai maksimum f(x,y) = x + y pada himpunan A = {x ≥ 0, y ≥ 0, x + 3y ≤ 6,3 x + y ≤ a} adalah 4, maka nilai a = …?
Penyelesaian
Misalkan f(x,y) = x + y
Pertidaksamaan-1: x + 3y ≤ 6
Pertidaksamaan-2: 3x + y ≤ a, x ≥ 0, dan y ≥ 0.
Gambar .Daerah penyelesaian untuk sistem pertidaksamaan linear x + 3y ≤ 6, 3x + y ≤ a
Mengingat gradien dari f(x,y) = x + y adalah m = –1, maka f akan mencapai maksimum di titik P. Titik P adalah perpotongan dari garis x + 3y = 6 dan 3x + y = a. Jadi diperoleh
Karena nilai maksimum f(x,y) = x + y adalah 4, maka
Dengan demikian, agar nilai maksimum f(x,y) = x + y adalah 4 maka nilai a = 10.
Untuk melihat barang-barang bagus dan murah silahkan cek:



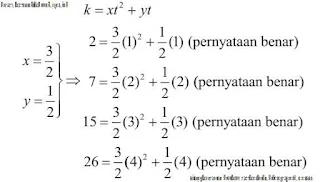









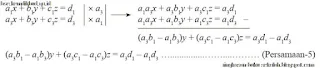










Komentar
Posting Komentar