Ringkasan Buku Sekolah
Kelas 10 (SMA / MA / SMK)
Matematika
Bab 1 Eksponen dan Logaritma
Latihan Soal dan Jawaban
Pegang teguh sifat matematika; yaitu, matematika bersandar pada kesepakatan, saling terkait materinya, menggunakan variabel-variabel, dan bersifat abstrak sebab matematika adalah hasil abstraksi pemikiran manusia. Matematika menganut kebenaran konsistensi; artinya, tidak boleh ada di dalamnya unsur-unsur, simbolsimbol, konsep-konsep, rumus-rumus yang saling bertentangan. Jika sebuah konsep ditemukan, ukuran kebenarannya adalah apabila konsep tersebut diterima pada struktur matematika yang sudah ada sebelumnya. Jika prinsip (rumus-rumus, sifat-sifat) yang ditemukan, ukuran kebenarannya dapat dibuktikan kebenarannya menggunakan konsep atau aturan yang sudah ada sebelumnya.
Gambar .Grafik Fungsi Exponen
1. Menemukan Konsep Eksponen
Misalkan a bilangan real dan n bilangan bulat positif. aⁿ adalah hasil kali bilangan a sebanyak n faktor, dapat ditulis 
dengan a sebagai basis bilangan pokok dan n sebagai pangkat.
Catatan:
1. Pada Definisi-1.1 di atas, kita sepakati, a¹ cukup ditulis a.
2. Hati-hati dengan bilangan pokok a = 0, tidak semua a⁰ dengan a bilangan real hasilnya adalah 1. Coba tanyakan pada gurumu, mengapa demikian?
3. Jika n adalah sebuah variabel (variabel sebagai eksponen dari a), maka perlu dicermati semestanya dimana variabel itu dibicarakan. Sebab aⁿ = a × a × ... × a sebanyak n faktor, ini hanya berlaku ketika semesta n∈N.
Fungsi Eksponen adalah suatu fungsi yang dinyatakan dalam bentuk y = f(x) = a(bcx) dengan a, b, dan c bilangan real.
x adalah variabel
b adalah bilangan pokok atau basis
c adalah koefisien x
cx adalah eksponen dari b.
2. Pangkat Bulat Negatif
Untuk a bilangan real dan a ≠ 0, m bilangan bulat positif, didefinisikan
3. Pangkat Nol
Untuk a bilangan real dan a ≠ 0, maka a⁰ = 1.
4. Sifat-sifat Pangkat Bulat Positif
Sifat-1
Jika a bilangan real, m dan n bilangan bulat positif maka
am × an = am+n
Bukti:
Sifat-2
Jika a bilangan real dan a ≠ 0, m dan n bilangan bulat positif, maka
Bukti:
Sifat-3
Jika a bilangan real dan a ≠ 0, m dan n adalah bilangan bulat positif, maka (am)n = amn
Bukti:
Misalkan a bilangan real dan a ≠ 0, m, n bilangan bulat positif didefinisikan
Misalkan ⁿ√a bilangan real dan n bilangan bulat positif. disebut bentuk akar jika dan hanya jika hasil ⁿ√a adalah bilangan irrasional.
Hubungan Bentuk Akar dan Bilangan Berpangkat
Operasi Penjumlahan dan Pengurangan Bentuk Akar
Operasi penjumlahan dan pengurangan pada bentuk akar dapat dilakukan apabila
bentuk akarnya senama. Bentuk akar senama adalah bentuk akar yang mempunyai
eksponen dan basis sama. Untuk setiap p, q, dan r adalah bilangan real dan r ≥ 0
berlaku sifat-sifat berikut.
Operasi Perkalian dan Pembagian Bentuk Akar
Pada pangkat pecahan telah dinyatakan bahwa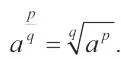 
Kita tahu bahwa bentuk-bentuk akar seperti , dst
merupakan bilangan irrasional. Jika bentuk akar tersebut menjadi penyebut pada
suatu pecahan, maka dikatakan sebagai penyebut irasional.
Merasionalkan bentuk
Bentuk tersebut dirasionalkan dengan cara mengalikannya dengan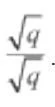
Merasionalkan bentuk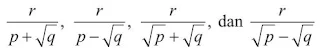
dapat dilakukan dengan memperhatikan sifat perkalian (a + b) (a – b) = a² – b².
Menemukan Konsep Logaritma
Telinga manusia dapat mendengar suara dengan intensitas yang rentangnya luar
biasa. Suara paling keras yang dapat didengar oleh orang yang sehat tanpa merusak
gendang telinga memiliki intensitas 1 triliun (1.000.000.000.000) kali lebih kuat dari
pada suara paling rendah yang bisa didengar.
Menghitung intensitas bunyi dengan rentang begitu besar tentu sangat tidak
nyaman. Namun, dengan logaritma perhitungan ini akan menjadi lebih sederhana.
Logaritma merupakan suatu operasi hitung. Alexander Graham Bell (1847–1922)
menggunakan logaritma untuk menghitung skala bunyi. Skala ini dinamakan
decibel, dan didefinisikan sebagai 
dengan D adalah skala decibel
bunyi, I adalah intensitas bunyi dengan satuan Watt per meter persegi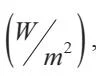
dan Io adalah intensitas bunyi paling minimum yang bisa didengar orang yang sehat, yaitu
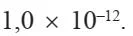
Tabel .Intensitas bunyi beberapa suara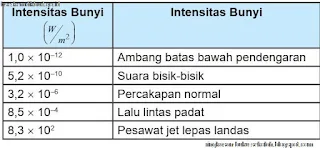
Misalkan a, b, c ∈ R, , , dan b > 0 maka alog b = c jika dan hanya jika ac = b.
dimana: a disebut basis (0 < a < 1 atau a > 1)
b disebut numerus (b > 0)
c disebut hasil logaritma
Gambar .Grafik Fungsi Logaritma
Sifat Dasar Logaritma
Misalkan a dan n bilangan real, a > 0 dan a ≠ 1, maka
1. ᵃlog a = 0
2. ᵃlog 1 = 0
3. ᵃlog an = n
Untuk a, b, dan c bilangan real positif, a ≠ 1, dan b > 0, berlaku
ᵃlog(b*c) = ᵃlogb + ᵃlogc
Untuk a, b, dan c bilangan real dengan a > 0, a ≠ 1, dan b > 0, berlaku
ᵃlog(b/c) = ᵃlogb - ᵃlogc
Untuk a, b, dan n bilangan real, a > 0, b > 0, a ≠ 1, berlaku
ᵃlogbⁿ= nᵃlogb
Untuk a, b, dan c bilangan real positif, a ≠ 1, b ≠ 1, dan c ≠ 1, berlaku
Untuk a, b, dan c bilangan real positif dengan a ≠ 1 dan c ≠ 1, berlaku
Untuk a dan b bilangan real positif dengan a ≠ 1, berlaku
dengan m, n bilangan bulat dan m ≠ 0.
Untuk a dan b bilangan real positif a ≠ 1, berlaku
MATERI-MATERI LAINNYA :
Untuk melihat barang-barang bagus dan murah silahkan cek:
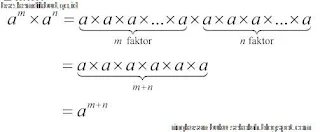
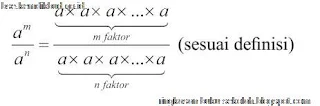
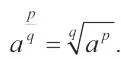
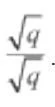
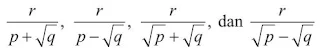
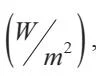
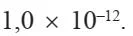
Komentar
Posting Komentar