Ringkasan Buku Sekolah
Kelas 10 (SMA / MA / SMK)
MATEMATIKA
Bab 9 Geometri
Latihan Soal dan JawabanTitik, Garis dan Bidang
Definisi
1) Jika suatu titik dilalui garis, maka dikatakan titik terletak pada garis tersebut.
2) Jika suatu titik tidak dilalui garis, maka dikatakan titik tersebut berada di luar garis.
3) Jika suatu titik dilewati suatu bidang, maka dikatakan titik itu terletak pada bidang.
4) Jika titik tidak dilewati suatu bidang, maka titik itu berada di luar bidang.
Tentunya panjang ketiga segmen AB, BC, dan AC memenuhi Theorema Phytagoras.
Titik A, B, dan C adalah titik-titik sudut segitiga ABC dan siku-siku di C, maka jarak antara titik A dan B adalah:
Jarak Titik ke Garis
Terdapat dua kemungkinan titik pada garis, yaitu titik terletak pada garis atau titik berada di luar garis. Titik dikatakan terletak pada garis, jika titik tersebut dilalui oleh garis. Dalam hal ini, jarak titik ke garis adalah nol.
Jarak Titik Ke Bidang
Misalkan X adalah suatu bidang datar, dan titik P merupakan sebuah titik yang berada diluar bidang X. Jarak antara titik P terhadap bidang X, merupakan jarak titik P ke tiitk berat bidang X.
Gambar .Jarak Titik Ke Bidang
Jarak antara Dua Garis dan Dua Bidang yang Sejajar
Garis k dan l dikatakan sejajar jika jarak antara kedua garis tersebut selalu sama (konstan), dan jika kedua garis tidak berhimpit, maka kedua garis tidak pernah berpotongan meskipun kedua garis diperpanjang.
Gambar .Dua garis sejajar, k dan l dipotong secara tegak lurus oleh garis m
Menemukan Konsep Sudut pada Bangun Ruang
Sifat dua garis dalam satu bidang yang sama
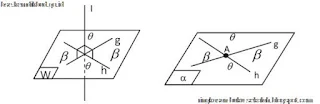
Misalkan garis k dan garis l berpotongan secara sembarang, maka pasangan sudut yang dihasilkan (ada dua pasang) besarnya sama.
Gambar .dua garis dalam satu bidang yang sama
Pada kubus ABCD.EFGH, berlaku.
1. Titik E terletak pada garis AE, EF, dan EH.
2. Garis EF terletak pada bidang ABFE dan EFGH.
3. Titik E terletak pada bidang ABFE, AEHD, EFGH yang memuat garis AE, EF, dan EH.
4. Garis EF dan garis CD adalah dua garis yang sejajar.
5. Garis AF dan garis BE adalah dua garis yang bersilangan.
6. Garis EF dan CG adalah dua garis yang saling tegak lurus.
7. Garis EF sejajar dengan salah satu garis pada bidang CDHG, maka garis EF sejajar dengan bidang CDGH.
8. Garis EF tegak lurus dengan salah satu garis pada bidang BCGF, maka garis EF tegak lurus dengan bidang BCGF.
9. Bidang ADHE berpotongan dengan bidang BCHE.
10. Bidang ABFE berpotongan tegak lurus dengan bidang ABCD.
11. Bidang ABFE sejajar dengan bidang CDHG.
12. Garis AF merupakan diagonal bidang ABFE 13. Garis BH merupakan diagonal ruang kubus ABCD, EFGH.
14. Bidang BCHE merupakan bidang diagonal.
15. ∠AUE = ∠BUF dan ∠AUB = ∠EUF.
16. Jarak antara dua titik adalah panjang ruas garis terpendek yang menghubungkan dua titik tersebut.
17. Jarak antara sebuah titik ke sebuah garis adalah jarak titik ke proyeksinya pada garis.
18. Jarak antara sebuah titik ke sebuah bidang adalah jarak titik ke proyeksinya pada bidang.
19. Jarak antara dua garis sejajar adalah jarak salah satu titik di salah satu garis ke garis yang lain.
20. Jarak dua garis bersilangan adalah panjang ruas garis yang tegak lurus pada kedua garis tersebut.
21. Jarak antara dua bidang yang sejajar adalah jarak dari salah satu titik pada bidang yang satu ke bidang yang lain.
22. Sudut antara garis dengan bidang adalah sudut antara garis tersebut dengan projeksinya pada bidang.
Demikianlah ringkasan / rangkuman dari Bab 9 Geometri, Matematika Kelas 10. Semoga dapat dimanfaatkan untuk materi pembelajaran adik-adik di waktu luangnya.
MATERI-MATERI LAINNYA :
Untuk melihat barang-barang bagus dan murah silahkan cek:
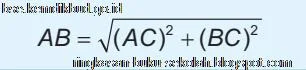






Komentar
Posting Komentar