Ringkasan Buku Sekolah
Kelas 9 (SMP/MTS)
MATEMATIKA
Bab 2 Persamaan dan Fungsi Kuadrat
Latihan Soal dan Jawaban
Persamaan t2 – 21t – 270 = 0 merupakan salah satu contoh persamaan kuadrat dan untuk menyelesaiakannya akan dibahas pada bagian ini. Secara umum persamaan kuadrat satu variabel adalah suatu persamaan yang pangkat tertingginya dua dan biasanya dituliskan sebagai ax2 + bx + c = 0 dengan a ≠ 0 dan a, b, c ∈ R. Bilangan a, b, c pada persamaan kuadrat tersebut disebut sebagai koefisien.
Akar-akar atau penyelesaian dari ax2+ bx + c = 0 adalah nilai x yang memenuhi persamaan tersebut.
Cara menentukan akar persamaan kuadrat ada tiga, yaitu:
(1) Memfaktorkan
(2) Melengkapi Kuadrat Sempurna (3) Rumus Kuadratik (Rumus abc)
Tahap inti dari metode ini adalah memfaktorkan persamaan kuadrat ax²+ bx + c = 0 menjadi bentuk kuadrat sempurna (x + p²+ q = 0 (jika diuraikan menjadi x2 + 2px + p2 + q = 0).
Untuk bentuk kuadrat sempurna, koefisien dari x2 adalah 1 maka persamaan kuadrat yang akan diselesaikan (ax²+ bx + c = 0) harus dibagi ... supaya koefisien dari x² juga 1. Sehingga didapat persamaan kuadrat baru yang ingin diselesaikan adalah x²+ b/a .x + c/a = 0. Langkah berikutnya adalah mencari nilai p dan q sedemikian hingga memenuhi
Jadi untuk membentuk kuadrat sempurna harus dicari bilangan p dan q sedemikian hingga p = b/2a dan q = c/a - (b /2a)²
Rumus kuadratik/rumus abc
Dan nilai di dalam akar disebut sebagai diskriminan (D) yaitu
D = b² – 4ac
Nilai diskriminan ini mempengaruhi penyelesaian/akar-akar dari persamaan kuadrat.
Grafik Fungsi Kuadrat
Fungsi kuadrat merupakan fungsi yang berbentuk y = ax² + bx + c, dengan a ≠ 0.
Grafik dari fungsi kuadrat menyerupai parabloa, sehingga dapat dikatakan juga sebagai fungsi parabola.
Gambar . Perbandingan Grafik fungsi kuadrat y = x², y = –x² dan y = 2x²
Nilai a pada fungsi y = ax² + bx + c akan mempengaruhi bentuk grafiknya. Jika a positif maka grafiknya akan terbuka ke atas. Sebaliknya jika a negatif maka grafiknya akan terbuka ke bawah. Jika nilai a semakin besar maka grafiknya menjadi lebih “kurus”.
Gambar .Perbandingan grafik fungsi kuadrat y = x + 2x, y = x² – 3x + 2 dan y = –x² – 5x – 4
Nilai b pada grafik y = ax² + bx + c menunjukkan letak koordinat titik puncak dan sumbu simetri (titik puncak dan sumbu simetri dibahas lebih lanjut pada subbab selanjutnya). Jika a > 0, grafik y = ax² + bx + c memiliki titik puncak minimum.
Jika a < 0, grafik y = ax² + bx + c memiliki titik puncak maksimum.
Nilai c pada grafik y = ax² + bx + c menunjukkan titik perpotongan grafik fungsi kuadrat tersebut dengan sumbu-y, yakni pada koordinat (0, c).
Menentukan Sumbu Simetri dan Titik Optimum
Fungsi kuadrat f(x) = ax² + bx + c mempunyai sumbu simetri
x = - b/a
Dengan nilai optimumnya adalah :
y₀ = - D / 4a
Langkah-langkah mensketsa grafik fungsi kuadrat:
Langkah 1. Menentukan bentuk parabola (terbuka ke atas atau ke bawah).
Langkah 2. Menentukan perpotongan grafik terhadap sumbu-x; yaitu, koordinat titik potongnya adalah (x₁, 0) yang memenuhi persamaan f(x₁) = 0
Langkah 3. Menentukan perpotongan grafik terhadap sumbu-y; yaitu, koordinat titik potongnya adalah (0, y₁) dengan y₁ didapatkan berdasarkan persamaan y₁ = f(0) Langkah 4. Menentukan sumbu simetri dan nilai optimum dari grafik fungsi.
Langkah 5. Mensketsa grafik fungsi kuadrat berdasarkan langkah (1), (2), (3), dan (4).
Menentukan Fungsi Kuadrat
Untuk menentukan fungsi kuadrat diperlukan beberapa informasi, di antaranya sebagai berikut.
1. Beberapa titik koordinat yang dilalui fungsi kuadrat tersebut.
2. Titik potong fungsi kuadrat tersebut di sumbu-x.
3. Titik potong fungsi kuadrat tersebut di sumbu-y.
4. Titik puncak dan sumbu simetri.
Kalau kamu suka membaca dan ingin mendapatkan buku sekolah di smartphone, kamu bisa download aplikasi android Buku Sekolah Gratis di playstore dari CTF Studio. Dengan menggunakan aplikasi ini kamu bisa membaca bukunya secara offline juga bila telah mendownloadnya atau secara online bila tidak mau menyimpan banyak data di smartphone. Bila berganti buku dan kamu ingin melanjutkan membacanya, kamu tidak perlu mencari halaman yang sebelumnya, jadi tinggal melanjutkan bacaannya saja.
MATERI-MATERI LAINNYA :
Untuk melihat barang-barang bagus dan murah silahkan cek:

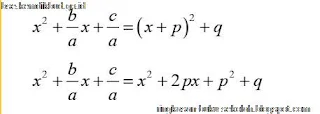






Komentar
Posting Komentar