Postingan Terbaru

Gunung Lewotobi Laki-laki Erupsi, Ribuan Penduduk Mengungsi

-
Gunung Lewotobi Laki-laki Erupsi, Ribuan Penduduk Mengungsi Gunung Lewotobi Laki-laki yang berada di Pulau Flores, Nusa Tenggara Timur, kembali mengalami peningkatan aktivitas vulkanik sejak akhir Maret 2025. Letusan yang terjadi pada 21 Maret memuntahkan kolom abu vulkanik setinggi lebih dari 8 kilometer. Akibatnya, status gunung tersebut dinaikkan ke level paling tinggi dan ribuan warga yang bermukim di sekitar lereng gunung terpaksa dievakuasi. Letusan ini merupakan bagian dari rangkaian aktivitas vulkanik yang sudah berlangsung sejak Desember 2023. Puncak letusan besar sempat terjadi pada awal November 2024 yang mengakibatkan korban jiwa sebanyak 10 orang, menghancurkan ribuan bangunan, dan membuat puluhan ribu warga harus mengungsi. Selain itu, abu vulkanik dari letusan tersebut juga berdampak pada penerbangan di Bali dan wilayah sekitarnya. Sebagai langkah antisipasi, pemerintah menetapkan zona larangan beraktivitas dalam radius 7 kilometer dari kawah. Otoritas setempat juga bere...
0

BAB 1 Dimensi Tiga - Matematika Kelas 12 SMA / MA / SMK

-

Ringkasan Buku Sekolah
Kelas 12 (SMA / MA / SMK)
MATEMATIKA
BAB 1 Dimensi Tiga


Latihan Soal dan Jawaban


Untuk menghemat biaya pembuatan rumah, salah satu aspek yang harus diperhatikan adalah biaya pembuatan kuda-kuda rumah. Penentuan Rincian Anggaran (RAB) pembuatan kuda-kuda dapat ditentukan dengan matematika


Gambar .Ruangan Atap Sumber: https://septanabp.wordpress.com/tag/attic/

Untuk mendapatkan rincian biaya tersebut, salah satu konsep yang dapat digunakan adalah dimensi tiga. Konsep yang dimaksud jarak titik dengan titik atau titik dengan garis.

Gambar . Kuda-kuda suatu rumah Sumber: http://www.megatrussglobal.com/2014/04/analisis-perbandingan-harga-konstruksi.html

Rumus Jarak Antar Titik

Gambar .Tampilan Layar Radar
Titik dalam radar tersebut merepresentasikan objek yang dideteksi radar.

Titik pusat radar adalah lokasi sinyal radar dipancarkan. Untuk menentukan jarak suatu benda, ternyata dapat digunakan rumus matematika.

Gambar .Segitiga siku-siku ACB

Panjang AB dapat dihitung dengan menggunakan teorema Pythagoras.

Jarak Titik ke Garis

Tabel .Jarak titik ke garis pada bangun ruang.


Masalah

Diberikan kubus ABCD.EFGH sebagai berikut. Jika panjang rusuk kubus adalah 2 cm, berapakah jarak titik A ke diagonal bidang EB ?

Alternatif Penyelesaian

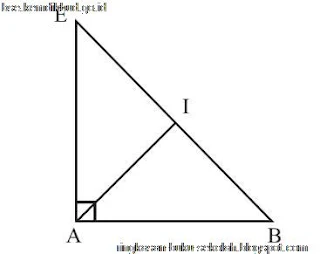
Jika titik E dan B dihubungkan dengan ruas garis, maka diperoleh, 

Jarak titik A ke EB adalah panjang ruas garis AI dengan BI = 1/2 BE, mengapa?

Jarak Titik ke Bidang

Tabel .Jarak titik ke bidang

Masalah

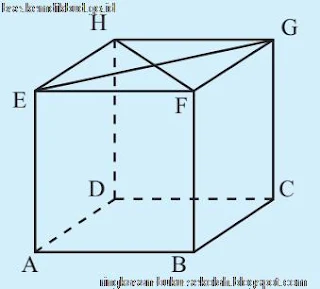
Diberikan kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik A, F, G, dan D dihubungkan sehingga terbentuk bidang AFGD seperti gambar di samping. Berapakah jarak titik B ke bidang AFGD?

Gambar .Bidang AFGD pada Kubus ABCD.EFGH

Alternatif Penyelesaian

Untuk menentukan jarak titik B ke bidang AFGD dapat ditentukan dengan mencari panjang ruas garis yang tegak lurus dengan bidang AFGD dan melalui titik B.

BT tegak lurus dengan bidang AFGD, sehingga jarak titik B ke bidang AFGD adalah panjang ruas garis BT . Titik T adalah titik tengah diagonal bidang AF (mengapa?). Panjang AF adalah 4√2 cm, sehingga panjang AT adalah 2√2 cm.

Karena BT tegak lurus bidang AFGD, maka segitiga ATB adalah segitiga siku-siku. Sehingga: 

Jadi jarak titik B ke bidang AFGD adalah 2√2 cm.


MATERI-MATERI LAINNYA :

Komentar

Posting Komentar

Postingan Populer

Gambar

Bab VII Menilai Karya Melalui Resensi Kelas 11 (SMA / MA) Bahasa Indonesia

Ringkasan Buku Sekolah     Kelas 11 (SMA / MA)   Bahasa Indonesia Bab VII Menilai Karya Melalui Resensi Latihan Soal dan Jawaban Resensi adalah ulasan atau penilaian atau pembicaraan mengenai suatu karya baik itu buku, film, atau karya lain. Tugas penulis resensi adalah memberikan gambaran kepada pembaca mengenai suatu karya apakah layak dibaca atau tidak. Hal-hal yang dapat ditanggapi dalam resensi ialah kualitas isi, penampilan, unsur-unsur, bahasa, dan manfaat bagi pembaca. Unsurunsur atau sistematika yang terdapat dalam resensi di antaranya sebagai berikut. 1. Judul resensi 2. Identitas buku yang diresensi 3. Pendahuluan (memperkenalkan pengarang, tujuan pengarang buku, dan lain-lain) 4. Inti/isi resensi 5. Keunggulan buku 6. Kekurangan buku 7. Penutup Isi Informasi Buku yang Diresensi Berdasarkan objek karyanya, resensi terdiri atas bermacam-macam jenis. Seperti yang terdapat di dalam contoh di atas, ada resensi untuk novel; ada pula yang berupa kumpulan ce...
Gambar

BAB II. PERMAINAN BOLA KECIL - PJOK Kelas 8 SMP/MTS

Ringkasan Buku Sekolah Kelas 8 (SMP/MTS) PJOK BAB II. PERMAINAN BOLA KECIL Latihan Soal dan Jawaban Permainan Bola Kecil melalui Aktivitas Permainan Softball Permainan sofball lahir di Amerika Serikat, ditemukan di Gedung Olahraga Farragut Boat Club Chicago, Illinois pada 16 September 1887 secara tidak sengaja oleh George Hancock.  Gerak Spesifik 1. Gerak Spesifik Pelambung (Pitcher) Gambar .Prinsip dasar pelambung (pitcher) 2. Gerak Spesifik Memegang Tongkat/Stick Kayu Pemukul dengan Kedua Tangan. Gambar .Memegang tongkat/stick kayu pemukul dipegang erat-erat dengan kedua tangan 3. Gerak Spesifik Memukul Swing Gambar .Prinsip dasar memukul Swing. 4. Gerak Spesifik Pukulan Tumbuk (Bunt) Gambar .Pukulan tumbuk (bunt) Variasi Gerak Spesifik Pembelajaran Softball Variasi dalam pembelajaran softball adalah melakukan satu bentuk gerak spesifik dengan berbagai cara, seperti: melakukan gerak spesifik melambung/melempar bola di tempat, sambil bergerak maju-mundur, dan bergerak menyamping, ...
Gambar

Bab V Manajemen Pergelaran Tari - Seni Budaya Kurtilas Kelas 12 (SMA / MA / SMK)

Ringkasan Buku Sekolah Kelas 12 ( SMA / MA / SMK ) SENI BUDAYA  SEMESTER 1 Bab V Manajemen Pergelaran Tari  Gambar . Pergelaran Drama Tari Dewi Pangrenyep Gambar .Pergelaran Drama Tari Dewi Pangrenyep Peta Materi  Gambar .Peta Materi A Pengertian Manajemen Pergelaran Tari  Dalam sebuah proses berkesenian profesional dan modern, upaya seniman dalam mempublikasikan karyanya membutuhkan suatu konsep manajemen pergelaran yang mampu mengelola dan memasarkan produk karya seni yang diciptakannya kepada masyarakat.  Pada dasarnya, penerapan prinsip manajemen dalam seni tari lebih banyak diterapkan pada suatu kegiatan pergelaran tari yang memiliki nilai komersial atau ditiketkan.  Kata manajemen sendiri yang dalam bahasa inggris ditulis “management” (dan kata kerja to manage) berasal dari bahasa latin managiare atau dalam bahasa itali Maneggio yang artinya mengurusi, mengendalikan, atau “menangani”. Menurut Mary Parker Follet, management seni adalah suatu pekerjaan ...