RINGKASAN BUKU SEKOLAH
KELAS 7 (SMP/MTS)
MATEMATIKA
BAB 2 HIMPUNAN
Di dalam kehidupan sehari-hari, kata himpunan ini dipadankan dengan kumpulan, kelompok, grup, atau gerombolan. Dalam biologi misalnya, kita mengenal kelompok flora dan kelompok fauna. Di dalamnya, masih ada lagi kelompok vertebrata, kelompok invertebrata, kelompok dikotil, dan kelompok monokotil. Dalam kehidupan sehari-hari, kalian juga mengenal suku Jawa, suku Madura, suku Sasak, suku Dayak, suku Batak, dan lain-lain.
Semua itu merupakan kelompok. Istilah kelompok, kumpulan, kelas, maupun gerombolan dalam matematika dikenal dengan istilah himpunan.
Penyajian Himpunan
Cara 1: Dinyatakan dengan menyebutkan anggotanya (enumerasi)
Suatu himpunan dapat dinyatakan dengan menyebutkan semua
anggotanya yang dituliskan dalam kurung kurawal. Manakala banyak
anggotanya sangat banyak, cara mendaftarkan ini biasanya
dimodifikasi, yaitu diberi tanda tiga titik (“…”) dengan pengertian
“dan seterusnya mengikuti pola”.
Cara 2: Dinyatakan dengan menuliskan sifat yang dimiliki anggotanya
Suatu himpunan dapat dinyatakan dengan menyebutkan sifat yang
dimiliki anggotanya. Perhatikan himpunan pada Contoh 2.1 dan
bandingkan dengan contoh di bawah ini.
Cara 3: Dinyatakan dengan notasi pembentuk himpunan
Suatu himpunan dapat dinyatakan dengan menuliskan syarat
keanggotaan himpunan tersebut. Notasi ini biasanya berbentuk
umum {x | P(x)} dimana x mewakili anggota dari himpunan, dan
P(x) menyatakan syarat yang harus dipenuhi oleh x agar bisa
menjadi anggota himpunan tersebut. Simbol x bisa diganti oleh
variabel yang lain, seperti y, z, dan lain-lain. Misalnya A = {1, 2, 3, 4,
5} bisa dinyatakan dengan notasi pembentuk himpunan A = {x | x <
6, dan x ∈ asli}.
Lambang {x | x < 6, dan x ∈ asli} ini bisa dibaca sebagai “Himpunan
x sedemikian sehingga x kurang dari 6 dan x adalah elemen bilangan
asli}. Tetapi, jika kita sudah memahami dengan baik, maka lambang
ini biasanya cukup dibaca dengan “Himpunan bilangan asli kurang
dari 6”.

A dan B tidak beririsan
A dan B Beririsan
A bagian dari B
A dan B memiliki anggota yang sama
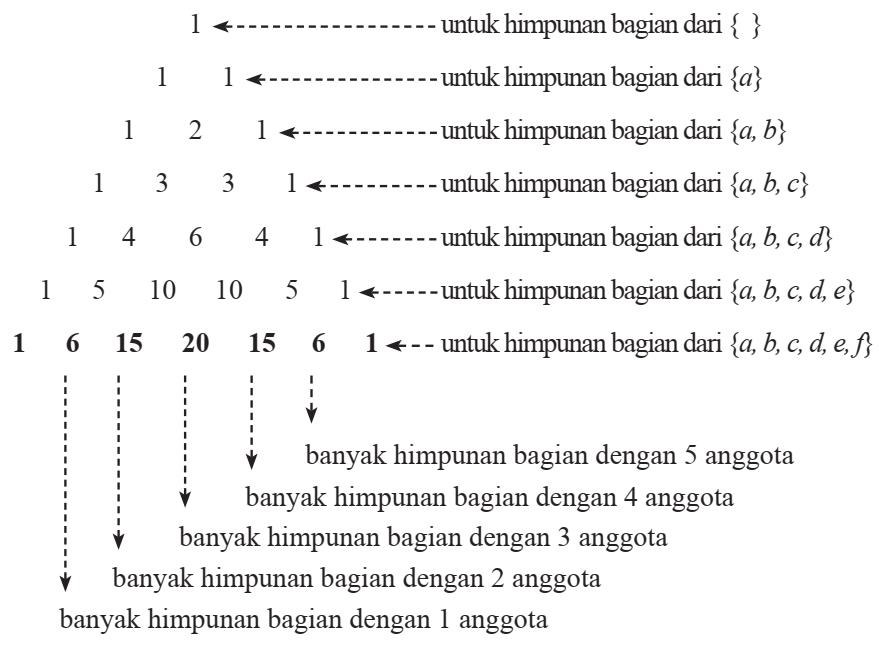
Kardinalitas Himpunan adalah bilangan yang menyatakan banyaknya anggota dari suatu himpunan dan dinotasikan dengan n(A).
Himpunan Kuasa dari himpunan A adalah himpunan-himpunan bagian dari A, dilambangkan dengan P(A). Banyak anggota himpunan kuasa dari himpunan A dilambangkan dengan n(P(A)).
Misalkan A himpunan dan P(A) adalah himpunan kuasa A.
Jika n(A) = n dengan n bilangan cacah, maka n(P(A)) = 2n
Macam-macam Diagram Venn
Macam-macam diagram venn lanjutan:
Demikianlah ringkasan mengenai Himpunan. Semoga bermanfaat ya....
Kalau kamu suka membaca dan ingin mendapatkan buku sekolah di smartphone, kamu bisa download aplikasi android di playstore dari CTF Studio. Dengan menggunakan aplikasi ini kamu bisa membaca bukunya secara offline juga bila telah mendownloadnya atau secara online bila tidak mau menyimpan banyak data di smartphone. Bila berganti buku dan kamu ingin melanjutkan membacanya, kamu tidak perlu mencari halaman yang sebelumnya, jadi tinggal melanjutkan bacaannya saja.
Untuk melihat barang-barang bagus dan murah silahkan cek:










Komentar
Posting Komentar